gallery_double_pendulum.cpp

Double Pendulum Simulation

This example demonstrates chaotic dynamics through real-time simulation of a double pendulum system, showcasing the complex, unpredictable motion that emerges from simple nonlinear differential equations and sensitive dependence on initial conditions.

Mathematical Framework

The double pendulum system is governed by the coupled nonlinear differential equations:

where:

• are the angles from vertical
• are the angular velocities
• are the pendulum lengths
• are the masses
• is gravitational acceleration

The state vector is with coordinate transformation: ,

What You'll Learn

• Implementing physics simulations with coupled nonlinear differential equations
• Using 4th-order Runge-Kutta (RK4) integration for accurate numerical solutions
• Visualizing chaotic systems with real-time trajectory tracking and trail visualization
• Working with canonical equations of motion for double pendulum dynamics
• Creating smooth physics animations with proper time stepping and state management
• Understanding conservation of energy in Hamiltonian systems with small damping
• Managing complex state vectors and multi-body mechanical system visualization

Sample Output

The example creates a real-time physics simulation featuring:

• Two connected pendulum masses with realistic physics (lengths m, masses kg)
• Gray connecting rods showing the physical linkage structure
• Red and blue markers representing the two pendulum masses
• Colored trails showing the historical motion paths of both masses
• Chaotic motion patterns that are highly sensitive to initial conditions
• Real-time updates at approximately 100 FPS for smooth animation
• Proper angle wrapping and energy-conserving integration

The system demonstrates classic chaotic behavior where small changes in initial conditions lead to dramatically different long-term evolution.

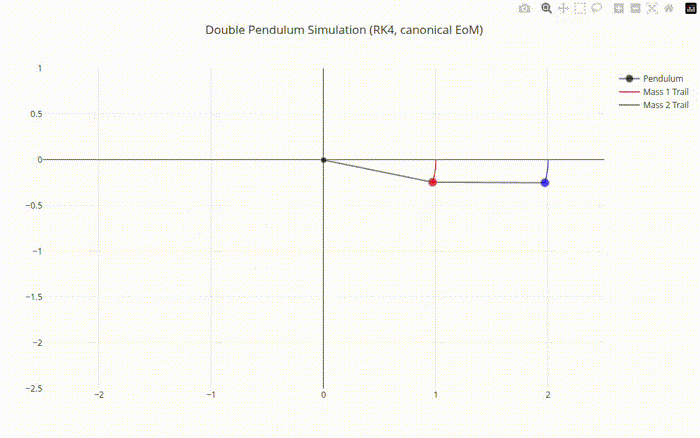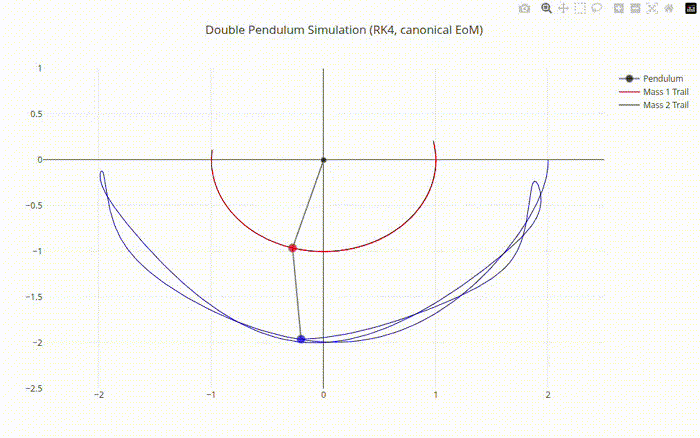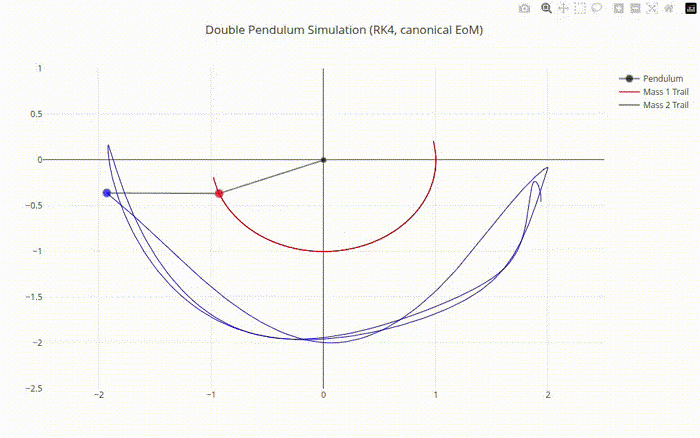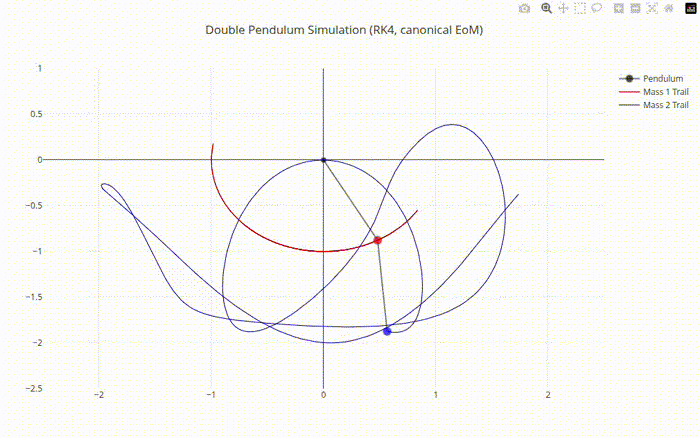
Double Pendulum Chaotic Motion Output

See also

plotly::Figure For the main plotting interface

plotly::Figure::update() For real-time plot updates during simulation

 
#include "plotly/plotly.hpp"
#include <array>
#include <chrono>
#include <cmath>
#include <cstddef>
#include <thread>
#include <vector>
 
// State vector: [theta1, theta2, omega1, omega2]
// theta measured from vertical-down, x = l*sin(theta), y = -l*cos(theta)
using State = std::array<double, 4>;
 
struct Params {
  double l1{1.0};   // length of pendulum 1
  double l2{1.0};   // length of pendulum 2
  double m1{1.0};   // mass of pendulum 1
  double m2{1.0};   // mass of pendulum 2
  double g{9.8};    // gravity
  double c1{0.002}; // small viscous damping for omega1 (optional)
  double c2{0.002}; // small viscous damping for omega2 (optional)
};
 
// Normalize angle to (-pi, pi]
inline auto wrapAngle(double x) -> double {
  return std::remainder(x, 2.0 * M_PI);
}
 
// Canonical double-pendulum accelerations for absolute angles from vertical
static inline auto accelerations(const State &s, const Params &p)
    -> std::array<double, 2> {
  const double th1 = s[0], th2 = s[1];
  const double w1 = s[2], w2 = s[3];
 
  const double d = th1 - th2;
  const double sd = std::sin(d);
  const double cd = std::cos(d);
  const double twoD = 2.0 * th1 - 2.0 * th2;
  const double denom0 = (2.0 * p.m1 + p.m2) - p.m2 * std::cos(twoD);
  const double den1 = p.l1 * denom0;
  const double den2 = p.l2 * denom0;
 
  const double num1 = -p.g * (2.0 * p.m1 + p.m2) * std::sin(th1) -
                      p.m2 * p.g * std::sin(th1 - 2.0 * th2) -
                      2.0 * sd * p.m2 * (w2 * w2 * p.l2 + w1 * w1 * p.l1 * cd);
 
  const double num2 =
      2.0 * sd *
      (w1 * w1 * p.l1 * (p.m1 + p.m2) + p.g * (p.m1 + p.m2) * std::cos(th1) +
       w2 * w2 * p.l2 * p.m2 * cd);
 
  double a1 = num1 / den1;
  double a2 = num2 / den2;
 
  // Small viscous damping (optional)
  a1 += -p.c1 * w1;
  a2 += -p.c2 * w2;
 
  return {a1, a2};
}
 
// Derivative function for RK4: f(t, y) -> dy/dt
static inline auto dynamics(const State &y, const Params &p) -> State {
  const auto acc = accelerations(y, p);
  return State{y[2], y[3], acc[0], acc[1]};
}
 
// Single RK4 step
static inline void rk4Step(State &y, double dt, const Params &p) {
  const State k1 = dynamics(y, p);
 
  State y2;
  for (int i = 0; i < 4; ++i)
    y2[i] = y[i] + 0.5 * dt * k1[i];
  const State k2 = dynamics(y2, p);
 
  State y3;
  for (int i = 0; i < 4; ++i)
    y3[i] = y[i] + 0.5 * dt * k2[i];
  const State k3 = dynamics(y3, p);
 
  State y4;
  for (int i = 0; i < 4; ++i)
    y4[i] = y[i] + dt * k3[i];
  const State k4 = dynamics(y4, p);
 
  for (int i = 0; i < 4; ++i) {
    y[i] += (dt / 6.0) * (k1[i] + 2.0 * k2[i] + 2.0 * k3[i] + k4[i]);
  }
 
  // Keep angles wrapped
  y[0] = wrapAngle(y[0]);
  y[1] = wrapAngle(y[1]);
}
 
auto main() -> int {
  Params p;
 
  // Integration settings
  const double dt = 0.003;        // integrator dt
  const int substepsPerFrame = 3; // RK4 substeps per animation frame
 
  // Initial conditions
  State s{};
  s[0] = M_PI / 2.0; // theta1
  s[1] = M_PI / 2.0; // theta2
  s[2] = 0.0;        // omega1
  s[3] = 0.0;        // omega2
 
  // Trails
  std::vector<double> x1Trail, y1Trail;
  std::vector<double> x2Trail, y2Trail;
  const int maxTrailLength = 500;
 
  // Plotly figure
  plotly::Figure fig;
  fig.openBrowser();
 
  auto computePositions = [&](const State &st) -> std::array<double, 4> {
    const double x1 = p.l1 * std::sin(st[0]);
    const double y1 = -p.l1 * std::cos(st[0]);
    const double x2 = x1 + p.l2 * std::sin(st[1]); // absolute angle for link 2
    const double y2 = y1 - p.l2 * std::cos(st[1]);
    return std::array<double, 4>{x1, y1, x2, y2};
  };
 
  auto pos = computePositions(s);
 
  // Initial plot
  fig.newPlot(
      {{{"x", {0.0, pos[0], pos[2]}},
        {"y", {0.0, pos[1], pos[3]}},
        {"mode", "lines+markers"},
        {"type", "scatter"},
        {"marker",
         {{"size", {8, 12, 12}}, {"color", {"black", "red", "blue"}}}},
        {"line", {{"color", "gray"}, {"width", 2}}},
        {"name", "Pendulum"}},
       {{"x", x1Trail},
        {"y", y1Trail},
        {"mode", "lines"},
        {"type", "scatter"},
        {"line", {{"color", "red"}, {"width", 1}}},
        {"name", "Mass 1 Trail"}},
       {{"x", x2Trail},
        {"y", y2Trail},
        {"mode", "lines"},
        {"type", "scatter"},
        {"line", {{"color", "blue"}, {"width", 1}}},
        {"name", "Mass 2 Trail"}}},
      {{"title", {{"text", "Double Pendulum Simulation (RK4, canonical EoM)"}}},
       {"xaxis", {{"title", "x"}, {"range", {-2.5, 2.5}}}},
       {"yaxis", {{"title", "y"}, {"range", {-2.5, 1.0}}}},
       {"showlegend", true},
       {"plot_bgcolor", "white"}});
 
  // Animation loop
  while (fig.isOpen()) {
    for (int i = 0; i < substepsPerFrame; ++i) {
      rk4Step(s, dt, p);
    }
 
    pos = computePositions(s);
    const double x1 = pos[0], y1 = pos[1], x2 = pos[2], y2 = pos[3];
 
    x1Trail.push_back(x1);
    y1Trail.push_back(y1);
    x2Trail.push_back(x2);
    y2Trail.push_back(y2);
 
    auto trim = [&](std::vector<double> &vx, std::vector<double> &vy) -> void {
      if (vx.size() > static_cast<size_t>(maxTrailLength)) {
        vx.erase(vx.begin());
        vy.erase(vy.begin());
      }
    };
    trim(x1Trail, y1Trail);
    trim(x2Trail, y2Trail);
 
    fig.update({{"x", {{0.0, x1, x2}, x1Trail, x2Trail}},
                {"y", {{0.0, y1, y2}, y1Trail, y2Trail}}});
 
    std::this_thread::sleep_for(std::chrono::milliseconds(10));
  }
 
  return 0;
}