gallery_duffing.cpp

Duffing Oscillator Ensemble Simulation

This example demonstrates the rich dynamics of the Duffing oscillator equation, a classic nonlinear system exhibiting complex behaviors including chaos, through the evolution of many oscillators with random initial conditions in phase space.

What You'll Learn

• Implementing the Duffing equation:
• Using 4th-order Runge-Kutta integration for nonlinear differential equations
• Visualizing phase space dynamics with many-particle ensemble simulations
• Understanding nonlinear oscillator behavior with cubic restoring forces
• Creating real-time animations of complex dynamical systems evolution
• Exploring the effects of damping, nonlinearity, and periodic forcing
• Working with parameter regimes that exhibit chaotic and regular motion

Sample Output

The example creates a dynamic phase space visualization featuring:

• 1000 Duffing oscillators with random initial conditions distributed in
• Real-time evolution showing complex trajectories in position-velocity phase space
• Parameter values: (damping), (linear restoring), (cubic nonlinearity)
• External forcing: creating rich dynamical behavior
• Blue markers showing the instantaneous state of all oscillators
• Smooth animation revealing attractors, periodic orbits, and chaotic regions
• Phase space bounded visualization showing the full range of system dynamics

The Duffing oscillator serves as a paradigmatic example of deterministic chaos and demonstrates how simple nonlinear equations can produce highly complex behavior.

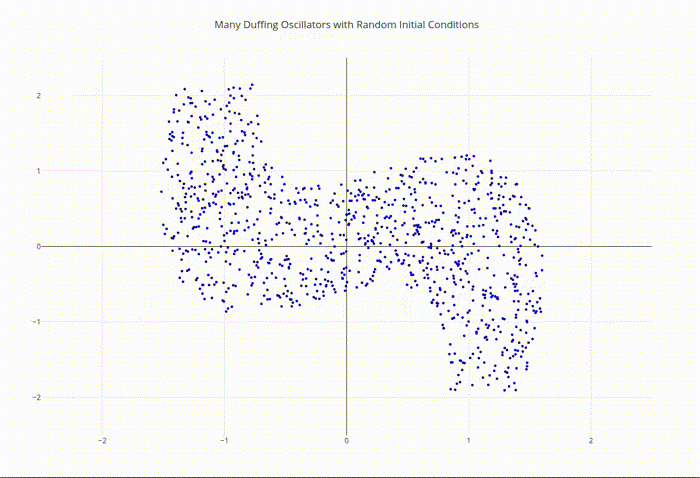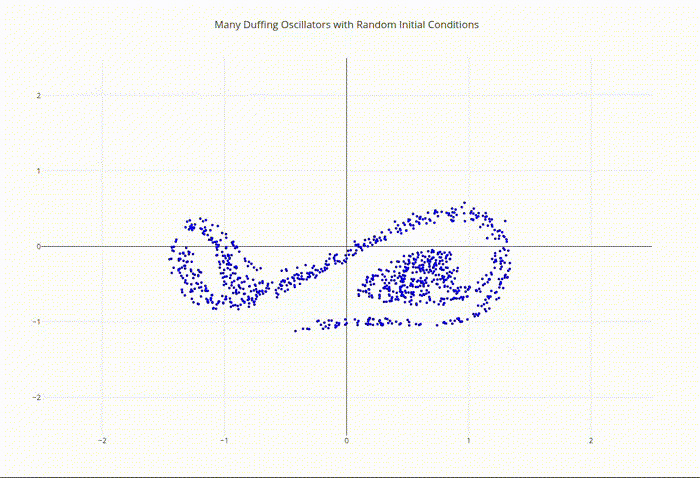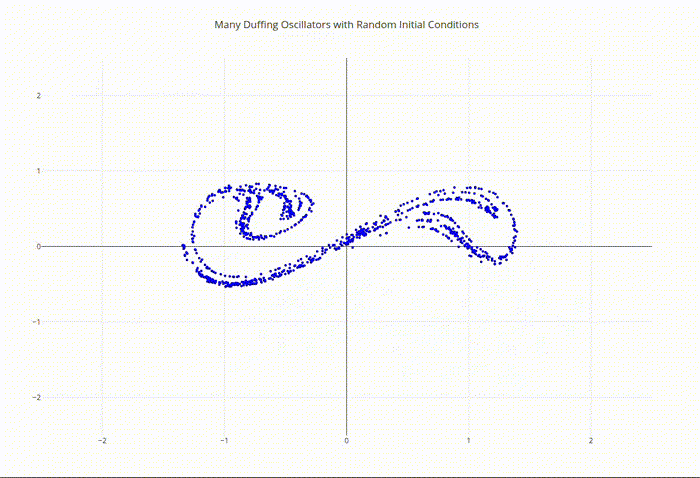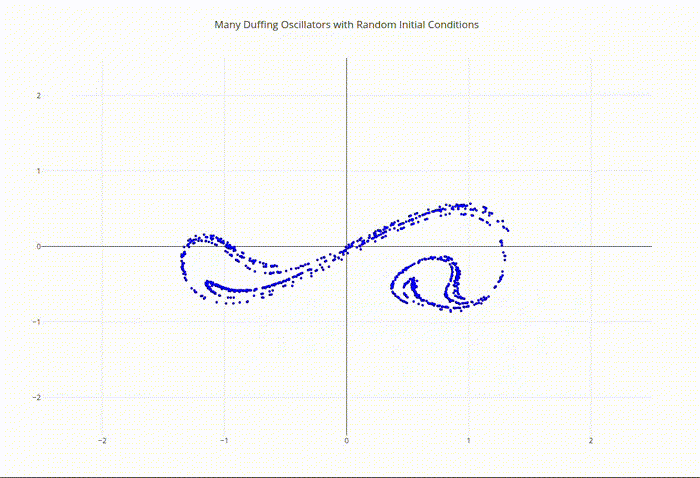
Duffing Oscillator Ensemble Phase Space Output

See also

plotly::Figure For the main plotting interface

plotly::Figure::update() For real-time phase space updates

 
#include "plotly/plotly.hpp"
#include <chrono>
#include <cmath>
#include <random>
#include <thread>
#include <utility>
#include <vector>
 
auto main() -> int {
  // Duffing equation parameters
  const double delta = 0.2;
  const double alpha = -1;
  const double beta = 1;
  const double gamma = 0.3;
  const double omega = 1.2;
 
  const int n = 1000; // Number of oscillators
  const double dt = 0.01;
  double t = 0;
 
  // Random number generation
  std::random_device rd;
  std::mt19937 gen(rd());
  std::uniform_real_distribution<double> posDist(-2.0, 2.0);
  std::uniform_real_distribution<double> velDist(-1.0, 1.0);
 
  // Random initial positions in [-2, 2] and velocities in [-1, 1]
  std::vector<double> xList(n);
  std::vector<double> vList(n);
 
  for (int i = 0; i < n; i++) {
    xList[i] = posDist(gen);
    vList[i] = velDist(gen);
  }
 
  // Duffing ODE derivatives
  auto f = [delta, alpha, beta, gamma,
            omega](double x, double v, double t) -> std::pair<double, double> {
    return {v, (-delta * v) - (alpha * x) - (beta * std::pow(x, 3)) +
                   (gamma * std::cos(omega * t))};
  };
 
  // 4th-order Runge-Kutta integration step
  auto rk4Step = [&f](double x, double v, double t,
                      double dt) -> std::pair<double, double> {
    auto [dx1, dv1] = f(x, v, t);
    auto [dx2, dv2] = f(x + (dx1 * dt / 2), v + (dv1 * dt / 2), t + (dt / 2));
    auto [dx3, dv3] = f(x + (dx2 * dt / 2), v + (dv2 * dt / 2), t + (dt / 2));
    auto [dx4, dv4] = f(x + (dx3 * dt), v + (dv3 * dt), t + dt);
 
    double xNew = x + (dt / 6 * (dx1 + 2 * dx2 + 2 * dx3 + dx4));
    double vNew = v + (dt / 6 * (dv1 + 2 * dv2 + 2 * dv3 + dv4));
 
    return {xNew, vNew};
  };
 
  // Create a plotly figure
  plotly::Figure fig;
  fig.openBrowser();
 
  // Initial phase space plot
  fig.newPlot(
      {{{"x", xList},
        {"y", vList},
        {"mode", "markers"},
        {"type", "scatter"},
        {"marker", {{"size", 4}, {"color", "blue"}, {"showscale", false}}}}},
      {{"title",
        {{"text", "Many Duffing Oscillators with Random Initial Conditions"}}},
       {"xaxis", {{"title", "x"}, {"range", {-2.5, 2.5}}}},
       {"yaxis", {{"title", "v"}, {"range", {-2.5, 2.5}}}},
       {"showlegend", false}});
 
  // Time evolution and update
  while (fig.isOpen()) {
    // Simulate 5 steps to speed up
    for (int step = 0; step < 5; step++) {
      for (int i = 0; i < n; i++) {
        auto [x_new, v_new] = rk4Step(xList[i], vList[i], t, dt);
        xList[i] = x_new;
        vList[i] = v_new;
      }
      t += dt;
    }
 
    // Update the plot
    fig.update({{"x", {xList}}, {"y", {vList}}});
 
    // Sleep for 30 milliseconds (like the JavaScript setInterval)
    std::this_thread::sleep_for(std::chrono::milliseconds(30));
  }
 
  return 0;
}