gallery_clustering_animation.cpp

K-means Clustering Animation

This example demonstrates the K-means clustering algorithm through real-time animation, visualizing how the algorithm iteratively converges to optimal cluster assignments by alternating between assignment and centroid update steps.

What You'll Learn

• Implementing the complete K-means clustering algorithm with iterative convergence
• Creating real-time animations that update plot elements dynamically during computation
• Visualizing machine learning algorithm convergence through interactive plots
• Managing multiple data traces (points and centroids) with different visual properties
• Using color coding to represent cluster assignments and algorithm state
• Applying mathematical distance calculations (Euclidean) for cluster assignment
• Implementing convergence detection and algorithm termination conditions

Sample Output

The example creates an animated visualization of K-means clustering with:

• 200 synthetic data points distributed across 4 natural clusters
• 4 cluster centroids (marked with X symbols) that move during optimization
• Real-time color updates showing point-to-cluster assignments
• Convergence detection that stops animation when algorithm reaches optimum
• Final visualization highlighting the discovered cluster structure

The algorithm demonstrates the two-step process:

1. Assignment step: Points change color based on nearest centroid
2. Update step: Centroids move to cluster centers

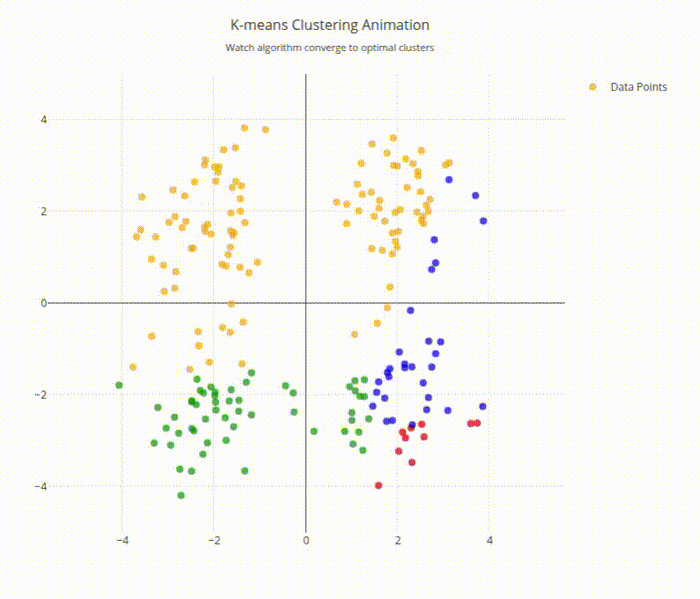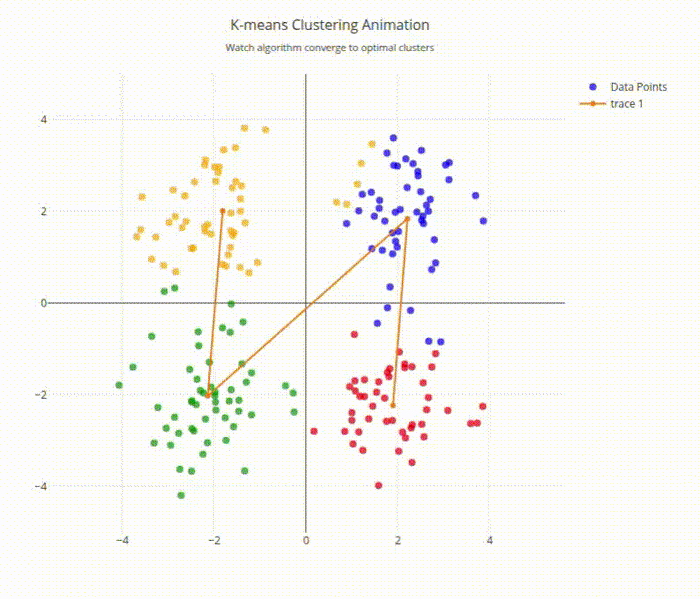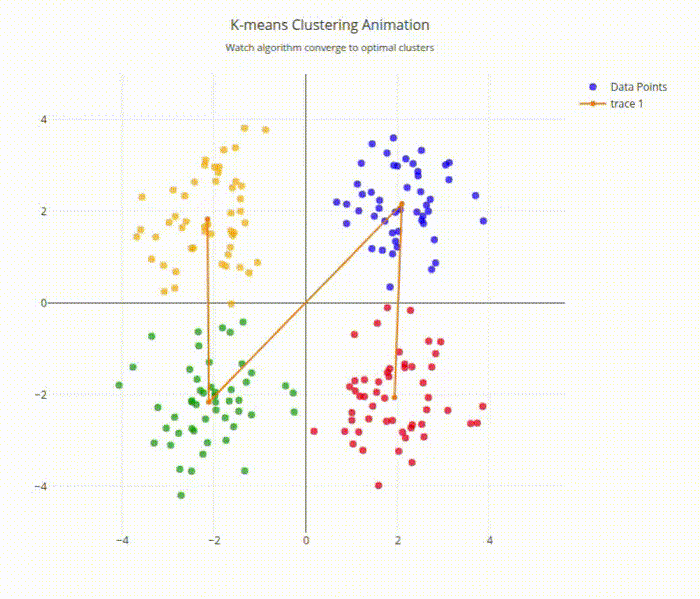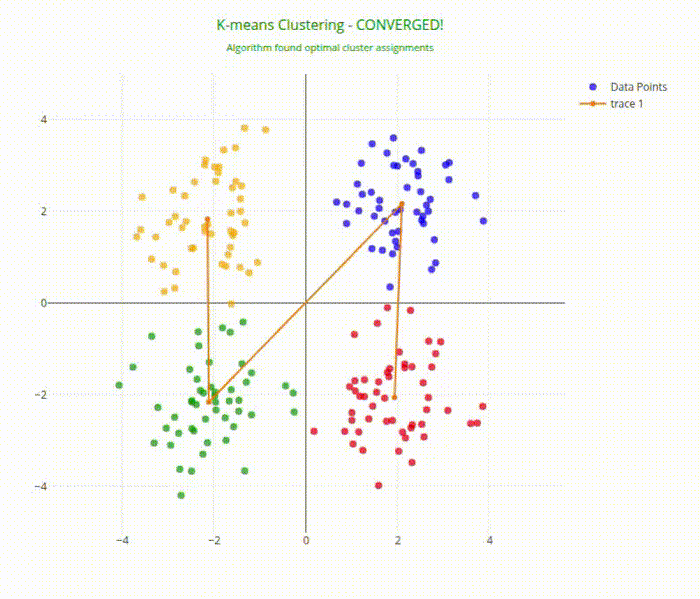
K-means Clustering Animation Output

See also

plotly::Figure For the main plotting interface

plotly::Figure::restyle() For updating plot properties during animation

 
#include "plotly/plotly.hpp"
#include <chrono>
#include <cmath>
#include <iostream>
#include <limits>
#include <random>
#include <string>
#include <thread>
#include <utility>
#include <vector>
 
struct Point {
  double x, y;
  int cluster;
  std::string color;
};
 
struct Centroid {
  double x, y;
  std::string color;
};
 
// Calculate Euclidean distance
auto distance(const Point &p, const Centroid &c) -> double {
  return std::sqrt((p.x - c.x) * (p.x - c.x) + (p.y - c.y) * (p.y - c.y));
}
 
auto main() -> int {
  std::cout << "Starting K-means clustering animation..." << '\n';
  plotly::Figure fig;
  fig.openBrowser();
 
  // Clustering parameters
  const int numPoints = 200;
  const int k = 4; // Number of clusters
  const int maxIterations = 20;
 
  std::vector<std::string> clusterColors = {"red", "blue", "green", "orange"};
 
  // Generate synthetic data with natural clusters
  std::random_device rd;
  std::mt19937 gen(rd());
 
  std::vector<Point> points;
  points.reserve(numPoints);
 
  // Create 4 natural clusters
  std::vector<std::pair<double, double>> clusterCenters = {
      {2.0, 2.0}, {-2.0, 2.0}, {-2.0, -2.0}, {2.0, -2.0}};
 
  for (int cluster = 0; cluster < 4; cluster++) {
    std::normal_distribution<double> xDist(clusterCenters[cluster].first, 0.8);
    std::normal_distribution<double> yDist(clusterCenters[cluster].second, 0.8);
 
    for (int i = 0; i < numPoints / 4; i++) {
      points.push_back({xDist(gen), yDist(gen),
                        -1, // Initially unassigned
                        "gray"});
    }
  }
 
  // Initialize centroids randomly
  std::uniform_real_distribution<double> coordDist(-4.0, 4.0);
  std::vector<Centroid> centroids(k);
  for (int i = 0; i < k; i++) {
    centroids[i] = {
        .x = coordDist(gen), .y = coordDist(gen), .color = clusterColors[i]};
  }
 
  // Create initial plot data
  std::vector<double> xCoords, yCoords;
  std::vector<std::string> pointColors;
  for (const auto &p : points) {
    xCoords.push_back(p.x);
    yCoords.push_back(p.y);
    pointColors.emplace_back("gray");
  }
 
  std::vector<double> centroidX, centroidY;
  std::vector<std::string> centroidColors;
  for (const auto &c : centroids) {
    centroidX.push_back(c.x);
    centroidY.push_back(c.y);
    centroidColors.push_back(c.color);
  }
 
  // Create traces
  plotly::Object pointTrace = {
      {"type", "scatter"},
      {"mode", "markers"},
      {"x", xCoords},
      {"y", yCoords},
      {"marker", {{"color", pointColors}, {"size", 8}, {"opacity", 0.7}}},
      {"name", "Data Points"},
      {"hovertemplate", "Point (%{x:.2f}, %{y:.2f})<extra></extra>"}};
 
  plotly::Object centroidTrace = {
      {"type", "scatter"},
      {"mode", "markers"},
      {"x", centroidX},
      {"y", centroidY},
      {"marker",
       {{"color", centroidColors},
        {"size", 20},
        {"symbol", "x"},
        {"line", {{"width", 3}, {"color", "black"}}}},
       {"name", "Centroids"},
       {"hovertemplate", "Centroid (%{x:.2f}, %{y:.2f})<extra></extra>"}}};
 
  // Create layout
  plotly::Object layout = {
      {"title",
       {{"text",
         "K-means Clustering Animation<br>" +
             std::string(
                 "<sub>Watch algorithm converge to optimal clusters</sub>")},
        {"font", {{"size", 16}}}}},
      {"xaxis",
       {{"title", "X Coordinate"}, {"range", {-5, 5}}, {"showgrid", true}}},
      {"yaxis",
       {{"title", "Y Coordinate"},
        {"range", {-5, 5}},
        {"showgrid", true},
        {"scaleanchor", "x"}}},
      {"width", 800},
      {"height", 700},
      {"showlegend", true}};
 
  // Create initial plot
  std::vector<plotly::Object> data = {pointTrace, centroidTrace};
  fig.newPlot(data, layout);
 
  std::cout << "Starting K-means algorithm with " << k << " clusters..."
            << '\n';
 
  // K-means algorithm with animation
  for (int iteration = 0; iteration < maxIterations; iteration++) {
    std::cout << "Iteration " << (iteration + 1) << "/" << maxIterations
              << '\n';
 
    bool converged = true;
 
    // Assignment step: assign each point to nearest centroid
    for (auto &point : points) {
      double minDist = std::numeric_limits<double>::max();
      int bestCluster = 0;
 
      for (int j = 0; j < k; j++) {
        double dist = distance(point, centroids[j]);
        if (dist < minDist) {
          minDist = dist;
          bestCluster = j;
        }
      }
 
      if (point.cluster != bestCluster) {
        converged = false;
        point.cluster = bestCluster;
        point.color = clusterColors[bestCluster];
      }
    }
 
    // Update point colors
    pointColors.clear();
    for (const auto &p : points) {
      pointColors.push_back(p.color);
    }
 
    // Update plot with new point assignments
    fig.restyle({{"marker.color", {pointColors}}}, {0});
 
    std::this_thread::sleep_for(std::chrono::milliseconds(800));
 
    // Update step: move centroids to cluster centers
    std::vector<double> newCentroidX(k, 0.0), newCentroidY(k, 0.0);
    std::vector<int> clusterCounts(k, 0);
 
    for (const auto &point : points) {
      if (point.cluster >= 0) {
        newCentroidX[point.cluster] += point.x;
        newCentroidY[point.cluster] += point.y;
        clusterCounts[point.cluster]++;
      }
    }
 
    // Calculate new centroid positions
    for (int j = 0; j < k; j++) {
      if (clusterCounts[j] > 0) {
        double newX = newCentroidX[j] / clusterCounts[j];
        double newY = newCentroidY[j] / clusterCounts[j];
 
        if (std::abs(centroids[j].x - newX) > 0.01 ||
            std::abs(centroids[j].y - newY) > 0.01) {
          converged = false;
        }
 
        centroids[j].x = newX;
        centroids[j].y = newY;
      }
    }
 
    // Update centroid positions
    centroidX.clear();
    centroidY.clear();
    for (const auto &c : centroids) {
      centroidX.push_back(c.x);
      centroidY.push_back(c.y);
    }
 
    fig.restyle({{"x", {centroidX}}, {"y", {centroidY}}}, {1});
 
    std::this_thread::sleep_for(std::chrono::milliseconds(800));
 
    if (converged) {
      std::cout << "Algorithm converged after " << (iteration + 1)
                << " iterations!" << '\n';
      break;
    }
  }
 
  // Update title to show completion
  fig.relayout(
      {{"title",
        {{"text",
          "K-means Clustering - CONVERGED!<br>" +
              std::string(
                  "<sub>Algorithm found optimal cluster assignments</sub>")},
         {"font", {{"size", 16}, {"color", "green"}}}}}});
 
  std::cout << "Clustering animation completed. Close browser to exit." << '\n';
  fig.waitClose();
 
  return 0;
}